问题
解答题
设函数f(x)=x3+ax2-a2x+1,g(x)=ax2-2x+1,其中实数a≠0。
(1)若a>0,求函数f(x)的单调区间;
(2)当函数y=f(x)与y=g(x)的图象只有一个公共点且g(x)存在最小值时,记g(x)的最小值为h(a),求h(a)的值域;
(3)若f(x)与g(x)在区间(a,a+2)内均为增函数,求a的取值范围。
答案
解:(1)∵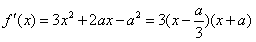
又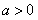
∴当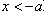 或
或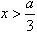 时,
时, ;
;
当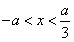 时,
时,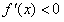
∴ 在
在 和
和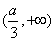 内是增函数,在
内是增函数,在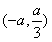 是减函数。
是减函数。
(2)由题意知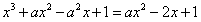 ,
,
即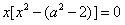 恰有一根(含重根)
恰有一根(含重根)
∴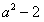 ≤0,
≤0,
即-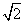 ≤a≤
≤a≤ ,
,
又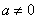 ,
,
∴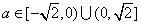
当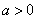 时,
时, 才存在最小值,
才存在最小值,
∴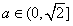
∵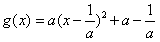 ,
,
∴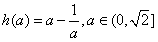
∴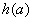 的值域为
的值域为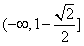 。
。
(3)当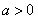 时,
时,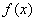 在
在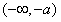 和
和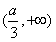 内是增函数,g(x)在
内是增函数,g(x)在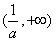 内是增函数
内是增函数
由题意得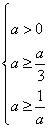 ,解得a≥1;
,解得a≥1;
当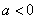 时,f(x)在
时,f(x)在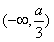 和
和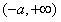 内是增函数,g(x)在
内是增函数,g(x)在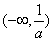 内是增函数
内是增函数
由题意得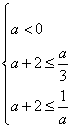 ,解得a≤-3;
,解得a≤-3;
综上可知,实数a的取值范围为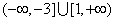 。
。
