问题
解答题
已知函数f（x）=ax3+bx2+c（a，b，c∈R，a≠0）的图象过点P（-1，2），且在点P 处的切线与直线x-3y=0垂直。
（1）若c=0，试求函数f（x）的单调区间；
（2）若a>0，b>0且（-∞，m），（n，+∞）是f（x）的单调递增区间，试求n-m-2c的范围。
答案
解：（1）由f（x）=ax3+bx2+c的图象过点P（-1，2）知-a+b+c=2
又f'（x）=3ax2+2bx
因为f（x）在点P处的切线与x-3y=0垂直，
所以3a-2b=-3
又c=0，解得a=1，b=3，
所以f'（x）=3x2+6x
令f'（x）=0得x1=0，x2=-2
显然，当x>0或x＜-2时，f'（x）>0，
-2＜x＜0时，f'（x）＜0，
所以（-∞，-2），（0，+∞）是f（x）的单调递增区间，
（-2，0）是 f（x）的单调递减区间。
（2）令f'（x）=3ax2+2bx=0，得x1=0，
又因为a>0，b>0，
所以当x>0或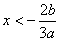
时，f'（x）>0，
即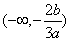
，（0，+∞）是f（x）的单调递增区间，
所以
由（1）知：-a+b+c=2且3a-2b=-3，
所以a=1-2c>0，b=3-3c>0，
∴
，
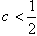∴1-2c∈（0，+∞）
∴
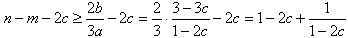
所以n-m-2c≥2，
即n-m-2c的范围是[2，+∞）。