解：（1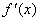）=3ax²+2bx-3，

依题意，f′(1)=f′(-1)=0，

即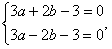解得a=1，b=0，

∴f（x）=x³-3x。

（2）∵f(x)=x³-3x，

∴f ′(x)=3x²-3=3(x+1)(x-1)，

当-1＜x＜1时，f ′(x)＜0，故f(x)在区间[-1，1]上为减函数，

f_max(x)=f(-1)=2，f_min(x)=f(1)=-2，

∵对于区间[-1，1]上任意两个自变量的值x₁，x₂，

都有|f(x₁)-f(x₂)|≤|f_max(x) -f_min(x)|，

∴ |f(x₁)-f(x₂)|≤|f_max(x)-f_min(x)|=2-(-2)=4。

（3）f′(x)=3x²-3=3(x+1)(x-1)，

∵曲线方程为y=x³-3x，

∴点A（1，m）不在曲线上，

设切点为M（x₀，y₀），则点M的坐标满足，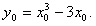

因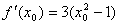，故切线的斜率为，

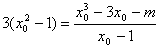整理得，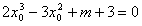

∵过点A（1，m）可作曲线的三条切线，

设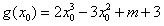，则，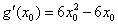

由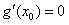，得x₀=0或x₀=1，

∴g(x₀)在（-∞，0），（1，+∞）上单调递增，在（0，1）上单调递减，

∴函数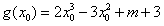的极值点为x₀=0，x₀=1，

∴关于x₀方程有三个实根的充要条件是，解得-3＜m＜-2，

故所求的实数a的取值范围是-3＜m＜-2。