问题
解答题
已知函数f(x)=(x2-ax)e-x(a∈R)。
(1)当a=2时,求函数f(x)的单调递减区间;
(2)若函数f(x)在(-1,1)上单调递减,求a的取值范围;
(3)函数f(x)可否为R上的单调函数,若是,求出a的取值范围,若不是,请说明理由.
答案
解:(1)当a=2时,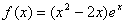 ,
,
∴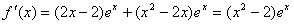 ,
,
令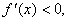 即
即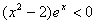 ,
,
∴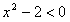 ,∴
,∴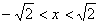 ,
,
∴函数f(x)的单调递减区间是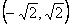 。
。
(2)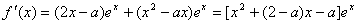 ,
,
∵f(x)在(-1,1)上单调递减,∴x∈(-1,1)时,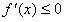 恒成立,
恒成立,
即x∈(-1,1)时,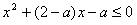 恒成立,
恒成立,
即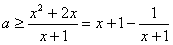 对一切x∈(-1,1)恒成立,
对一切x∈(-1,1)恒成立,
令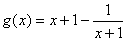 ,
,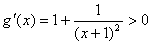 ,
,
∴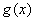 在(-1,1)上是增函数,
在(-1,1)上是增函数,
∴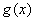
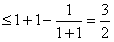 ,
,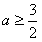 ,
,
即a的取值范围是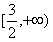 。
。
(3)∵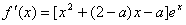 ,
,
设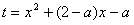 ,
,
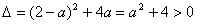 ,
,
∴x∈R时,t不恒为正值,也不恒为负值,
即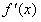 的值不恒正,也不恒负,
的值不恒正,也不恒负,
故f(x)在R上不可能单调。
