问题
选择题
A∈平面α.AB=5,AC=2
|
答案
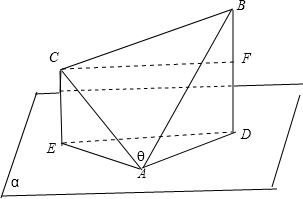
当B、C在平面α的同侧时如图作BD⊥α,垂足为D,作CE⊥α,垂足为E,连接AE,AD,DE,
过C作CF⊥BD,垂足为F,
则AD、AE分别为AB、AC在α内的射影,∴∠BAD,∠CAE分别为AB、AC与平面α所成的角,
∵AB与α所成角正弦值为0.8,AC与α成450角,
∴AE=CE=2,BD=4,AD=3,
设∠DAE=θ,BF=4-2
∴BC=
=CF2+BF2
=4+9+4-2×2×3×cosθ
,17-12cosθ
∵0≤θ≤π,∴
≤BC≤5 29
当B、C在平面α的异侧时,BF=4+2=6,
则BC=
=CF2+BF2
,36+9+4-2×2×3×cosθ
∵0≤θ≤π,∴
≤BC≤37
.61
故选D.