解：（Ⅰ）解：当t=1时，

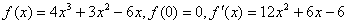
f′(0)=-6，

所以曲线y=f(x)在点(0，f(0))处的切线方程为y=-6x。

（Ⅱ）解：，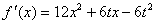

令f′(x)=0，解得x=-t或，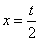

因为t≠0，以下分两种情况讨论：

（1）若t＜0，则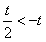，当x变化时，f′(x)，f(x)的变化情况如下表：

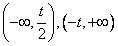
所以，f(x)的单调递增区间是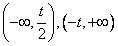；f(x)的单调递减区间是。

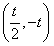（2）若t＞0，则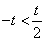，当x变化时，f′(x)，f(x)的变化情况如下表：

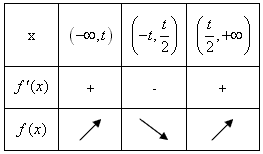
所以，f(x)的单调递增区间是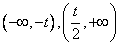；f(x)的单调递减区间是；

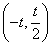（Ⅲ）证明：由（Ⅱ）可知，当t＞0时，f(x)在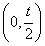内的单调递减，在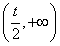内单调递增，以下分两种情况讨论：

（1）当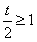即t≥2时，f(x)在（0，1）内单调递减，

，

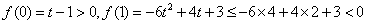所以对任意t∈[2，+∞)，f(x)在区间（0，1）内均存在零点；

（2）当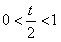即0＜t＜2时，f(x)在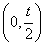内单调递减，在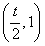内单调递增，

若，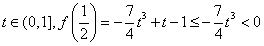

，

所以f(x)在内存在零点；

若，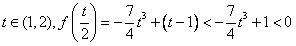

f(0)=t-1＞0，

所以f(x)在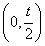内存在零点；

所以，对任意t∈(0，2)，f(x)在区间（0，1）内均存在零点。

综上，对任意t∈(0，+∞)，f(x)在区间（0，1）内均存在零点。