已知正方体ABCD-A1B1C1D1中，E，F分别为D1C1，C1B1的中点，A

问题证明题

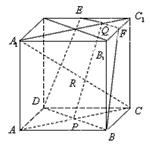
已知正方体ABCD-A₁B₁C₁D₁中，E，F分别为D₁C₁，C₁B₁的中点，AC∩BD=P，A₁C₁∩EF=Q，

求证：（1）D，B，F，E四点共面；

（2）若A₁C交平面DBFE于R点，则P，Q，R三点共线．

答案

证明：如图，

（1）∵EF是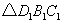的中位线，

∴，

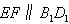在正方体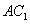中，，∴EF∥BD，

∴EF确定一个平面，即D，B，F，E四点共面．

（2）正方体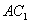中，设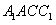确定的平面为α，又设平面BDEF为β，

，

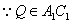∴Q∈α，

又Q∈EF，

∴Q∈β，则Q是α与β的公共点，α∩β=PQ，

又，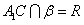

∴R∈A₁C，

∴R∈α，且R∈β，则R∈PQ，故P，Q，R三点共线。