解：(1)由题意得f′(x)=3x²+2bx-3，

因为函数f(x)在区间[1，+∞)上单调递增，

所以，对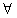x∈[1，+∞)恒成立，

所以对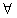x∈[1，+∞)恒成立，

令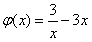，则，所以当x∈[1，+∞)时，ψ′(x)＜0恒成立，

所以函数ψ(x)是[1，+∞)上的单调减函数，

所以当x∈[1，+∞)时，函数ψ(x)的最大值是ψ(1)=0，

故2b≥0，即b≥0，又因为b∈(-∞，0]，所以b=0，

∴f(x)=x³-3x。

(2)由(1)可得，f′(x)=3x²-3，由f′(x)=3x²-3=0解得x=±1，

∵f(-1)=2，f(1)=-2，

∴当x∈[-2，2]时，，

则对于区间[-2，2]上任意两个自变量的值x₁，x₂，都有，

所以c≥4，所以c的最小值为4。

(3)∵点M(2，m)(m≠2)不在曲线y=f(x)上，

∴设切点为(x₀，y₀)，则，

，

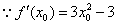∴切线的斜率为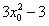，则，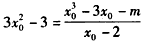

即，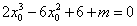

因为过点M(2，m)(m≠2)，可作曲线y=f(x)的三条切线，

所以方程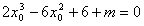有三个不同的实数解．

即函数有三个不同的零点，

则g′(x)=6x²-12x，令g′(x)=0，解得x=0或x=2，

由题意可得g(0)＞0，且g(2)＜0，

所以6+m＞0，且m-2＜0，解得：-6＜m＜2，

所以所求实数m的取值范围是-6＜m＜2。