问题
解答题
已知函数f(x)=ex(ax+1)(e为自然对数的底,a∈R为常数)。
(1)讨论函数f(x)的单调性;
(2)对于函数h(x)和g(x),若存在常数k,m,对于任意x∈R,不等式h(x)≥kx+m≥g(x)都成立,则称直线y=kx+m是函数h(x),g(x)的分界线,设a=1,问函数f(x)与函数g(x)=-x2+2x+1是否存在“分界线”?若存在,求出常数k,m。若不存在,说明理由。
答案
解:(1)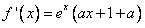
当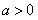 时,
时,
即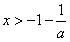
函数 在区间
在区间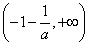 上是增函数,
上是增函数,
在区间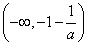 上是减函数;
上是减函数;
当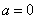 时,
时, ,函数
,函数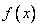 是区间
是区间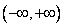 上的增函数;
上的增函数;
当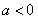 时,
时,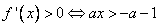
即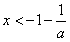
函数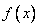 在区间
在区间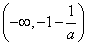 上是增函数,在区间
上是增函数,在区间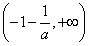 上是减函数。
上是减函数。
(2)若存在,则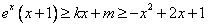 恒成立,
恒成立,
令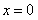 ,则
,则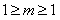 ,
,
所以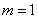
因此: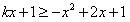 恒成立,即
恒成立,即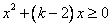 恒成立,
恒成立,
由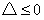 得到:
得到: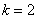 ,
,
现在只要判断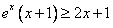 是否恒成立,
是否恒成立,
设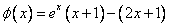 ,
,
因为: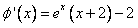 ,
,
当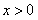 时,
时,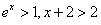 ,
,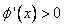 ,
,
当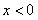 时,
时,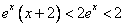 ,
,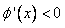 ,
,
所以: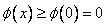 ,
,
即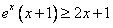 恒成立,
恒成立,
所以:函数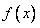 与函数
与函数 存在“分界线”,
存在“分界线”,
则 。
。
