问题
解答题
已知函数f(x)=xlnx。
(1)求这个函数的图象在点x=1处的切线方程;
(2)讨论这个函数的单调区间.
答案
解: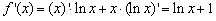 ,
,
(1)当x=1时,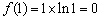 ,
, ,
,
所以,切线过点(1,0),斜率为1,
故切线的方程为y=x-1。
(2)令 ,即lnx+1>0,解得
,即lnx+1>0,解得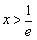 ;
;
所以,函数f(x)=xlnx的单调递增区间为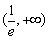 ;
;
令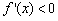 ,即lnx+1<0,解得
,即lnx+1<0,解得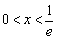 ;
;
所以,函数f(x)=xlnx的单调递减区间为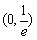 。
。
已知函数f(x)=xlnx。
(1)求这个函数的图象在点x=1处的切线方程;
(2)讨论这个函数的单调区间.
解: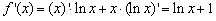 ,
,
(1)当x=1时,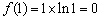 ,
, ,
,
所以,切线过点(1,0),斜率为1,
故切线的方程为y=x-1。
(2)令 ,即lnx+1>0,解得
,即lnx+1>0,解得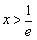 ;
;
所以,函数f(x)=xlnx的单调递增区间为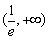 ;
;
令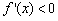 ,即lnx+1<0,解得
,即lnx+1<0,解得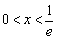 ;
;
所以,函数f(x)=xlnx的单调递减区间为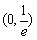 。
。