假设存在一个社会，这个社会由三个消费者组成，他们分别是1，2，3，同时该社会存在着两种商品，分别是x和y。经济学家Debreu对这三个消费者的消费行为进行分析，他认为1，2，3的偏好可以分别用如下的效用函数来表示：
①u1(x，y)=xy；
②u2(x，y)=xαyβ，其中α＞0，β＞O；
③u3=γlnx+(1-γ)lny，其中γ∈(0，1)。
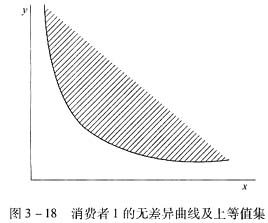
(1)请画出消费者1的无差异曲线以及偏好的上等值集；
(2)假如商品x和商品y的价格分别是2单位货币和3单位货币，同时消费者l拥有120单位货币，试计算他对x和y的最优消费量；
(3)证明：消费者2和消费者3的偏好是一致的；
(4)现在假设商品x和商品y的价格分别是p1和p2，消费者2拥有I单位货币，请计算他的消费选择；
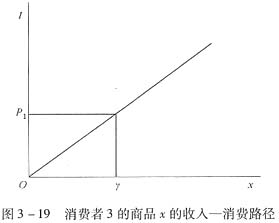
(5)用公式和图像给出消费者3对于x商品的收入一消费路径。
参考答案：解：(1)根据序数效用理论，无差异曲线是维持效用不变的商品组合的轨迹，偏好的上等值集就是无差异曲线右上方部分。根据消费者1的效用函数，其无差异曲线及上等值集如图3—18所示。
(2)消费者l的预算线方程：2x+3y=120。
由消费者l的效用函数，可得出商品x和y的边际效用，即MUx=y，MUy=x。
根据消费者效用最大化的一阶条件
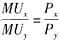，可得：
。
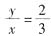将上式代入预算线方程，可得：x=30，y=20。
即消费者1对x和y的最优消费量为(30，20)。
(3)根据效用函数的性质：效用函数的线性变换依然是同一偏好的效用函数。对消费者2的效用函数进行取自然对数的线性变换，可得：lnu2=αlnx+βlny。
令α=γ，β=1-γ，因此。lnu2=γlnx+(1-γ)lny=u3。
因此，消费者2和消费者3的效用函数是同一偏好的效用函数，即消费者2和消费者3的偏好是一致的。
(4)消费者2的预算线方程：P1x+P2y=I。
由消费者2的效用函数，可得出商品x和y的边际效用，即MUx=αxα-1yβ，MUy=βxαyβ-1。
根据消费者效用最大化的一阶条件
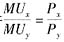，可得
。
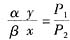将上式代入预算线方程，可得：
。
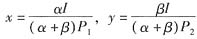即消费者2对z和y的最优消费量为
。
(5)消费者3的偏好和消费者2的偏好是一致的，因此消费者3的最优化问题和消费者2是相同的。
消费者3的恩格尔曲线方程为：
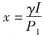，其中x的价格P1为常数。恩格尔曲线方程就是x商品的收入一消费路径．如图3—19所示。
