问题
解答题
已知函数f（x）=ln（ex+1）+ax，（a＜0）
（Ⅰ）若函数y=f（x）的导函数是奇函数，求a的值；
（Ⅱ）求函数y=f（x）的单调区间。
答案
解：（Ⅰ）f′(x)=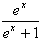
+a，
由f′(-x)=-f′(x)可解得：a=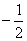
；
（Ⅱ）由已知，函数f(x)的定义域为R，
f′(x)=a+1-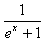
，
（1）当a+1≤0，即a≤-1时，f′(x)＜0恒成立，
∴a≤-1时，f(x)在R上为减函数；
（2）当a+1＞0，即-1＜a＜0时，由f′(x)＜0得：x＜ln
，
由f′(x)＞0得：x＞ln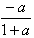
，
∴-1＜a＜0时，f(x)在（-∞，ln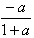
）上为减函数，在（ln
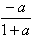，+∞）上为增函数；
综上可知a≤-1时，f(x)在R上为减函数；-1＜a＜0时，f(x)的单调减区间为（-∞，ln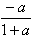
），单调增区间为（ln
，+∞）。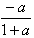