解：（Ⅰ）f（x）的导数，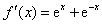

由于，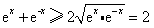

故f′（x）≥2，（当且仅当x=0时，等号成立）。

（Ⅱ）令g（x）=f（x）-ax，

则，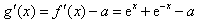

（ⅰ）若a≤2，当x＞0时，，

故g（x）在（0，+∞）上为增函数，

所以，x≥0时，g（x）≥g（0），即f（x）≥ax；

（ⅱ）若a＞2，方程g′（x）=0的正根为，

此时，若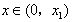，则g′（x）＜0，故g（x）在该区间为减函数，

所以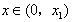，时，g（x）＜g（0）=0，即f（x）＜ax，与题设f（x）≥ax相矛盾；

综上，满足条件的a的取值范围是(-∞，2]。