问题
解答题
已知函数f(x)=alnx+x2(a为实常数),
(Ⅰ)若a=-2,求证:函数f(x)在(1,+∞)上是增函数;
(Ⅱ)求函数f(x)在[1,e]上的最小值及相应的x值.
答案
解:(Ⅰ)当a=-2时,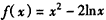 ,
,
当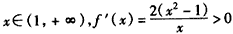 ,
,
故函数f(x)在(1,+∞)上是增函数。
(Ⅱ)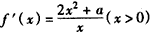 ,
,
当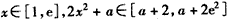 ,
,
ⅰ)若a≥-2,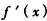 在[1,e]上非负(仅当a=-2,x=1时,
在[1,e]上非负(仅当a=-2,x=1时,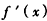 =0),
=0),
故函数f(x)在[1,e]上是增函数,此时,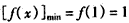 。
。
ⅱ)若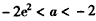 ,当
,当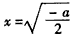 时,
时,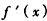 =0,
=0,
当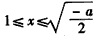 时,
时,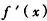 <0,此时f(x)是减函数;
<0,此时f(x)是减函数;
当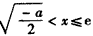 时,
时,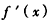 >0,此时f(x)是增函数;
>0,此时f(x)是增函数;
故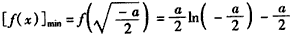 ;
;
ⅲ)若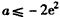 ,
,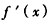 在[1,e]上非正(仅当a=-2e2,x=e时,
在[1,e]上非正(仅当a=-2e2,x=e时,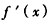 =0),
=0),
故函数f(x)在[1,e]上是减函数,此时,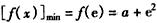 ;
;
综上可知,当a≥2时,f(x)的最小值为1,相应的x值为1;
当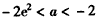 时,f(x)的最小值为
时,f(x)的最小值为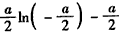 ,相应的x值为
,相应的x值为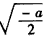 ;
;
当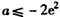 时,f(x)的最小值为
时,f(x)的最小值为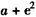 ,相应的x值为e。
,相应的x值为e。
