问题
解答题
已知函数f(x)=(a+1)lnx+ax2+1，
(Ⅰ)讨论函数f(x)的单调性；
(Ⅱ)设a＜-1，如果对任意x1，x2∈(0，+∞)，|f(x1)-f(x2)|≥4|x1-x2|，求a的取值范围。
答案
解：(Ⅰ)f(x)的定义域为(0，+∞)，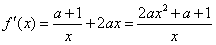
，
当a≥0时，f′(x)＞0，故f(x)在(0，+∞)单调增加；
当a≤-1时，f′(x)＜0，故f(x)在(0，+∞)单调减少；
当-1＜a＜0时，令f′(x)=0，解得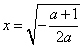
，
则当x∈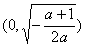
时，f′(x)＞0；x∈
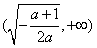时，f′(x)＜0，
故f(x)在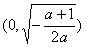
单调增加，在
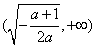单调减少．
(Ⅱ)不妨假设x1≥x2，而a＜-1，
由(Ⅰ)知f(x)在(0，+∞)单调减少，从而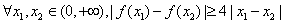
，
等价于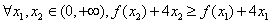
，①
令g(x)=f(x)+4x，则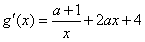
，
①等价于g(x)在(0，+∞)单调减少，即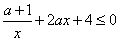
，
从而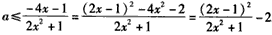
；
故a的取值范围为（-∞，-2]。