问题
解答题
求函数y=x2-lnx2的单调区间。
答案
解：∵函数y=f（x）=x2-lnx2的定义域为（-∞，0）∪（0，+∞），
又f′（x）=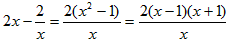
，
∴x，f′（x），f（x）的取值变化情况如下表：
由上表可知，函数f（x）=x2-lnx2在区间（-1，0），（1，+∞）上单调递增；在区间（-∞，-1），
（0，1）上单调递减。
搜题请搜索小程序“爱下问搜题”
求函数y=x2-lnx2的单调区间。
解：∵函数y=f（x）=x2-lnx2的定义域为（-∞，0）∪（0，+∞），
又f′（x）=，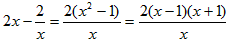
∴x，f′（x），f（x）的取值变化情况如下表：
由上表可知，函数f（x）=x2-lnx2在区间（-1，0），（1，+∞）上单调递增；在区间（-∞，-1），
（0，1）上单调递减。