问题
解答题
已知函数f(x)=x2-8lnx,g(x)=-x2+14x。
(1)求函数f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)与g(x)在区间(a,a+1)上均为增函数,求a的取值范围。
(3)若方程f(x)=g(x)+m有唯一解,试求实数m的值。
答案
解:(1)因为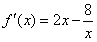
所以切线的斜率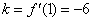
又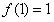
故所求切线方程为
即 。
。
(2)因为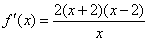
又x>0,所以当x>2时,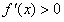 ;
;
当0<x<2时,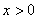
即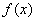 在
在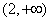 上递增
上递增
在(0,2)上递减
又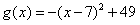
所以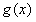 在
在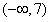 上递增
上递增
在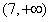 上递减
上递减
欲f(x)与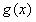 在区间
在区间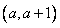 上均为增函数
上均为增函数
则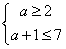
解得 。
。
(3)原方程等价于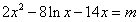
令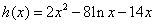
则原方程即为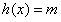
因为当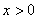 时原方程有唯一解
时原方程有唯一解
所以函数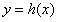 与
与 的图象在y轴右侧有唯一的交点
的图象在y轴右侧有唯一的交点
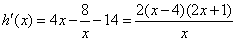 且x>0
且x>0
所以当x>4时,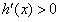
当0<x<4时,
即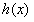 在
在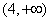 上递增
上递增
在(0,4)上递减
故h(x)在x=4处取得最小值
从而当时原方程有唯一解的充要条件是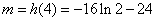 。
。
