问题
解答题
设函数f(x)=ax3+bx2-3a2x+1（a、b∈R）在x=x1，x=x2处取得极值，且|x1-x2|=2，
(Ⅰ)若a=1，求b的值，并求f(x)的单调区间；
(Ⅱ)若a＞0，求b的取值范围。
答案
解：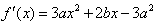
，①
（Ⅰ）当a=1时，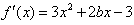
，
由题意知
为方程
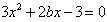的两根，
所以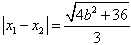
，
由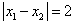
，得b=0，
从而f(x)=x3-3x+1，
，
当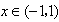
时，f′(x)＜0；当
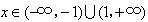时，f′(x)＞0，
故f(x)在（-1，1）单调递减，在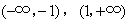
单调递增．
（Ⅱ）由①式及题意知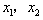
为方程
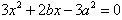的两根，
所以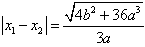
，
从而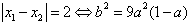
，
由上式及题设知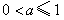
，
考虑
，
故g（a）在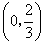
单调递增，在
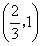单调递减，
从而g（a）在(0，1]的极大值为
，
又g（a）在(0，1]上只有一个极值，
所以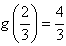
为g（a）在(0，1]上的最大值，且最小值为g（1）=0，
所以
，即b的取值范围为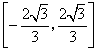
。