解：（1）由f（x）=e^x-2x+2a，x∈R知f'（x）=e^x-2，x∈R

令f'（x）=0，得x=ln2

于是，当x变化时，f'（x）和f（x）的变化情况如下表：

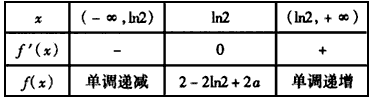
故f（x）的单调递减区间是（-∞，ln2），单调递增区间是（ln2，+∞）

f（x）在x=ln2处取得极小值

极小值为f（ln2）=2-2ln2+2a。

（2）证明：设g（x）=e^x-x²+20ax-1，x∈R，

于是g'（x）=e^x-2x+2a．x∈R

由（1）知当a>ln2-1时，g'（x）取最小值为g'（ln2）= 2（1-ln2+a）>0

于是对任意x∈R，都有g'（x）>0，

所以g（x）在R内单调递增，

于是，当a>ln2-1时，对任意x∈（0，+∞），都有g（x）>g（0），而g（0）=0

从而对任意x∈（0，+∞），都有g（x）>0

即e^x-x²+2ax-1>0，故e^x>x²-2ax+1。