解：函数f(x)的导数：，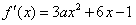

（Ⅰ）当f′（x）＜0（x∈R）时，f（x）是减函数，

，

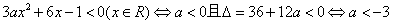所以，当a＜-3时，由f′（x）＜0，知f（x）（x∈R）是减函数；

（Ⅱ）当a=-3时，，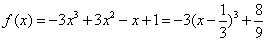

由函数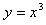在R上的单调性，

可知当a=-3时，f（x）（x∈R）是减函数；

（Ⅲ）当a＞-3时，在R上存在一个区间，其上有f′（x）＞0，

所以，当a＞-3时，函数f（x）（x∈R）不是减函数；

综上，所求a的取值范围是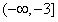。