解：（1）函数f（x）的定义域为R，

f′（x）=4x³-4x=4x（x²-1）=4x（x+1）（x-1），

令f′（x）＞0，则4x（x +1）（x-1）＞0，

解得-1＜x＜0或x＞1，

∴函数f（x）的单调递增区间为（-1，0）和（1，+∞），

令f′（x）＜0，则4x（x+1）（x-1）＜0，

解得x＜-1或0＜x＜1，

∴函数f（x）的单调递减区间为（-∞，-1）和（0，1）；

（2）函数的定义域为（0，+∞），其导数为，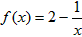

令f′（x）=2-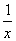＞0，

解得；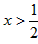

令，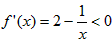

解得，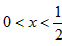

因此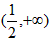为该函数的单调递增区间，在该区间上函数为增函数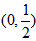，为该函数的单调递减区间，在该区间上函数为减函数。