解：(Ⅰ)由已知，得x＞0且f′(x)=，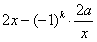

当k是奇数时，则f′(x)＞0，则f(x)在(0，+∞)上是增函数；

当k是偶数时，则f′(x)=，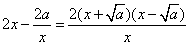

所以当x∈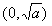时，f′(x)＜0，当x∈时，f′(x)＞0，

故当k是偶数时，f(x)在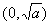上是减函数，在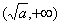上是增函数．

(Ⅱ)若k=2010，则f(x)=x²-2alnx(k∈N*)，

记g(x)=f(x)-2ax=x²-2alnx-20x，

g′(x)=，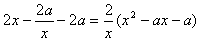

若方程f(x)=2ax有唯一解，即g(x)=0有唯一解；

令g′(x)=0，得x²-ax-a=0，

因为a＞0，x＞0，所以(舍去)，，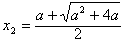

当x∈(0，x₂)时，g′(x)＜0，g(x)在(0，x₂)是单调递减函数；

当x∈(x₂，+∞)时，g′(x)＞0，g(x)在(x₂，+∞)上是单调递增函数．

当x=x₂时，g′(x₂)=0，g(x)_min=g(x₂)．

因为g(x)=0有唯一解，所以g(x₂)=0，

则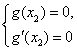，即，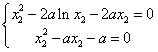

两式相减，得2alnx₂+ax₂-a=0，

因为a＞0，

∴2lnx₂+x₂-1=0， (*)

设函数h(x)=21nx+x-1，

因为在x＞0时，h(x)是增函数，所以h(x)=0至多有一解，

因为h(1)=0，

所以方程(*)的解为x₂=1，从而解得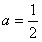。