问题
解答题
已知f(x)=x3+3ax2+bx+a2在x=-1时有极值0,
(1)求常数a、b的值;
(2)求f(x)的单调区间。
答案
解:(1)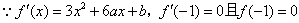 ,
,
∴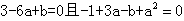 ,
,
∴ ;
;
(2)由(1)知当a=1,b=3时,
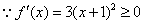 ,
,
∴f(x)在R上是增函数,即增区间为(-∞,+∞);
当a=2,b=9时,
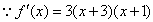 ,
,
∴在(-∞,-3)和(-1,+∞)上f′(x)>0,在(-3,-1)上f′(x)<0,
故当a=2,b=9时:增区间是(-∞,-3)和(-1,+∞),减区间是(-3,1)。
