问题
解答题
设a≥0,f (x)=x-1-ln2x+2a ln x(x>0)。
(1)令F(x)=xf'(x),讨论F(x)在(0,+∞)内的单调性并求极值;
(2)求证:当x>1时,恒有x>ln2x-2aln x+1。
答案
解:(1)根据求导法则有
故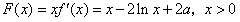
于是
列表如下:

故知F(x)在 内是减函数,在
内是减函数,在 内是增函数,
内是增函数,
所以,在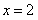 处取得极小值
处取得极小值 。
。
(2)由 知,
知,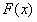 的极小值
的极小值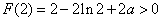
于是由上表知,对一切 ,恒有
,恒有
从而当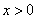 时,恒有
时,恒有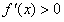 ,
,
故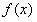 在
在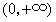 内单调增加
内单调增加
所以当 时,
时,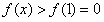 ,即
,即
故当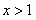 时,恒有
时,恒有 。
。
