问题
解答题
已知f(x)=x3+bx2+cx+d在(-∞,0]上是增函数,在(0,2]上是减函数,且f(x)=0有三个根α,2,β(α≤2≤β)。
(Ⅰ)求c的值,并求出b和d的取值范围;
(Ⅱ)求证:f(x)≥2;
(Ⅲ)求β-α的取值范围,并写出当β-α取最小值时的f(x)的解析式。
答案
解:(Ⅰ)因为f(x)在(-∞,0]上是增函数,在(0,2]上是减函数,
所以x=0是f′(x)=0的根,
又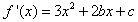 ,
,
由f′(0)=0,得c=0,
又f(x)=0的根是α,2,β,
所以f(2)=0,所以8+4b+d=0,
又f′(2)≤0,
所以12+4b≤0,所以b≤-3,
又d=-8-4b,
所以d≥4;
(Ⅱ)因为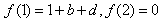 ,
,
所以d=-8-4b,且b≤-3,
所以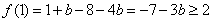 ;
;
(Ⅲ)因为f(x)=0有三个根α,2,β(α≤2≤β),
所以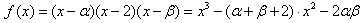 ,
,
所以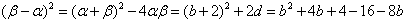
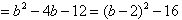 ,
,
又b≤-3,
所以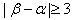 ,
,
当且仅当b=-3时取最小值,此时d=4,
所以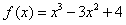 。
。
