解：（Ⅰ）由题意知f(1)=-3-c，因此b-c=-3-c，从而b=-3，

又对f(x)求导得，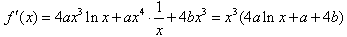

由题意f′(1)=0，

因此a+4b=0，解得a=12。

（Ⅱ）由（Ⅰ）知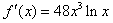（x＞0），

令f′(x)=0，解得x=1，

当0＜x＜1时，f′(x)＜0，此时f(x)为减函数；

当x＞1时，f′(x)＞0，此时f(x)为增函数；

因此f(x)的单调递减区间为（0，1），而f(x)的单调递增区间为（1，+∞）。

（Ⅲ）由（Ⅱ）知，f(x)在x=1处取得极小值f(1)=-3-c，此极小值也是最小值，

要使（x＞0）恒成立，只需，

即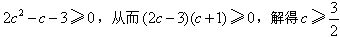或c≤-1，

所以c的取值范围为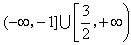。