There are two factors which determine an individual’s intelligence. The first is the sort of brain he is born with. Human brains differ considerably, some being more capable than others. But no matter how good a brain he has to begin with, an individual will have a low order of intelligence unless he has opportunities to learn. So the second factor is what happens to the individual—the sort of environment in which he is reared. If an individual is handicapped environmentally, it is likely that his brain will fail to develop and he will never attain the level of intelligence of which he is capable.
The importance of environment in determining an individual’s intelligence can be demonstrated by the case of the identical twins, Peter and Mark Being identical, the twins had identical brains at birth, and their growth processes were the same. When the twins were three months old, their parents died, and they were placed in separate foster homes. Peter was reared by parents of low intelligence in an isolated community with poor educational opportunities. Mark was reared in the home of well to do parents who had been to college. He was read to as a child, sent to good schools, and given every opportunity to be stimulated intellectually. This environmental difference continued until the twins were in their late teens, when they were given tests to measure their intelligence. Mark’s IQ was 125, twenty five points higher than the average and fully forty points higher than his identical brother. Given equal opportunities, the twins, having identical brains, would have tested at roughly the same level.
The best statement of the main idea of this passage is that ().
A.human brains differ considerably
B.the brain a person is born with is important in determining his intelligence
C.environment is crucial in determining a person’s intelligence
D.persons having identical brains will have roughly the same intelligence
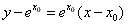
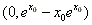
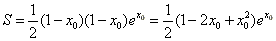
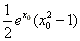
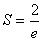
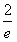 。
。