问题
解答题
三棱锥S-ABC中,侧棱SA、SB、SC两两互相垂直,M为三角形ABC的重心,D为AB的中点,作与SC平行的直线DP.
证明:
(1)DP与SM相交;
(2)设DP与SM的交点为D′,则D′为三棱锥S-ABC的外接球球心.
答案
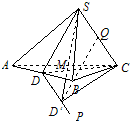
证明:(1)∵DP∥SC,故DP、CS共面.
∴DC⊂面DPC,
∵M∈DC,∴M∈面DPC,∴SM⊂面DPC.
∵在面DPC内SM与SC相交,故直线SM与DP相交.
(2)∵SA、SB、SC两两互相垂直,∴SC⊥面SAB,∴SC⊥SD.
∵DP∥SC,∴DP⊥SD,△DD′M∽△CSM.
∵M为△ABC的重心,∴DM:MC=1:2.∴DD′:SC=1:2.
取SC中点Q,连D′Q.则SQ=DD′,
∴SQ
DD′,SC⊥SD,∥ .
∴平面四边形DD′QS是矩形.
∴D′Q⊥SC,又SQ=QC,知D′C=D′S.
同理,D′A=D′B=D′C=D′S.
即以D′为球心D′S为半径作球D′,则A、B、C均在此球上.
即D′为三棱锥S-ABC的外接球球心.
