问题
解答题
已知函数f(x)=x3+bx2+ax+d的图象过点P(0,2),且在点M(﹣1,f(﹣1))处的切线方程为6x﹣y+7=0.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
答案
解:(Ⅰ)∵f(x)的图象经过P(0,2),
∴d=2,
∴f(x)=x3+bx2+ax+2,f'(x)=3x2+2bx+a.
∵点M(﹣1,f(﹣1))处的切线方程为6x﹣y+7=0
∴f'(x)|x=﹣1=3x2+2bx+a|x=﹣1=3﹣2b+a=6①,
还可以得到,f(﹣1)=y=1,即点M(﹣1,1)满足f(x)方程,
得到﹣1+b﹣a+2=1②
由①、②联立得b=a=﹣3
故所求的解析式是f(x)=x3﹣3x2﹣3x+2.
(Ⅱ)f'(x)=3x2﹣6x﹣3.
令3x2﹣6x﹣3=0,即x2﹣2x﹣1=0.
解得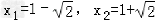 .
.
当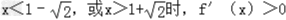 ;
;
当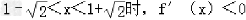 .
.
故f(x)的单调增区间为(﹣∞,1﹣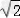 ),(1+
),(1+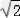 ,+∞);单调减区间为(1﹣
,+∞);单调减区间为(1﹣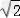 ,1+
,1+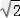 )
)