问题
证明题
已知x＞1，证明x＞ln（1+x）。
答案
证明：设f（x）=x-ln（1+x）（x＞1），
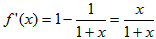
由x＞1，知f′（x）＞0，
∴f（x）在（1，+∞）上单调递增，
又f（1）=1-ln2＞0，即f（1）＞0，
∵x＞1，
∴f（x）＞0，即x＞ln（1+x）。
搜题请搜索小程序“爱下问搜题”
已知x＞1，证明x＞ln（1+x）。
证明：设f（x）=x-ln（1+x）（x＞1），
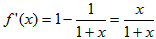
由x＞1，知f′（x）＞0，
∴f（x）在（1，+∞）上单调递增，
又f（1）=1-ln2＞0，即f（1）＞0，
∵x＞1，
∴f（x）＞0，即x＞ln（1+x）。
