问题
解答题
已知函数f（x）=ax-lnx，x∈(0，e]，其中e为自然常数，
（Ⅰ）当a=1时，求f（x）的单调区间和极值；
（Ⅱ）是否存在实数a，使得f（x）的最小值是3，若存在，求出a的值；若不存在，说明理由。
答案
解：（Ⅰ）a=1，f（x）=x-lnx，x∈(0，e]，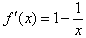
，
令f′（x）=0， 即：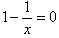
，解得x=1；
令f′（x）＞0， 即：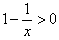
，解得1＜x≤e；
令f′（x）＜0， 即：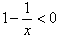
，解得0＜x＜1；
∴f（x）的单调增区间为(1，e]，单调减区间为（0，1），
f（x）在x=1处取得极小值为f（1）=1；
（Ⅱ）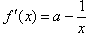
，
（1）若
，
∵x∈(0，e]，
∴f′（x）＜0，
∴f（x）在(0，e]上是减函数，
此时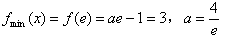
（舍）；
（2）若a＞0，令f′（x）=0，即：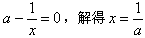
；
令f′（x）＞0，即：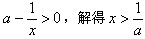
；
令f′（x）＜0，即：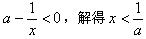
；
①若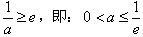
，此时f（x）在(0，e]上是减函数，
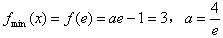（舍）；
②若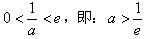
，此时f（x）在(0，e]上左减右增，
；
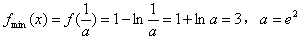综上可知：存在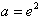
，使得f（x）的最小值是3。