问题
计算题
（17分）如图所示，在水平面上放置一凹槽B，B与水平面面间有摩擦，槽质量为m,内壁间距离为d，槽内靠近左侧壁处有质量也为m小物块A，带有q电量正电，槽内壁绝缘光滑，系统又处于一水平向右的匀强电场中，电场强度为E，t=0时刻A由静止释放，每次A与槽B内壁碰撞无动能损失交换速度。观察发现A只与槽B右壁发生周期性的碰撞，且每次碰后速度为零。求
（1）A第一次与槽B发生碰撞前的速度
（2）槽B与水平面间动摩擦因数μ
（3）以后运动过程中A与槽B左壁的最短距离和第n次碰撞前摩擦力对槽B所做功
答案
（1）
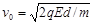（2）qE/2mg（3）-(n-1)qEd
（1）A碰前速度v0, 由动能定理
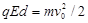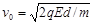（2分）
（2分）
(2)根据题意，保证周期性碰，每次A加速至v0,时，B刚好速度减到零，而A到达B右壁
所以AB加速度大小相等 aA=qE/m aB=2μmg/m （2分）
2μmg="qE " （2分）
得 μ="qE/2mg " （2分）
(3)每次当A加速到v0/2而B减速到v0/2时，A离左壁最近，设周期T为
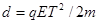
（2分）
A相对B右壁 x=3v0/4×T/2- v0 /4×T/2=d/2 （2分）
第n次碰前，B运动（n-1）d
Wf=-2μmg(n-1)d=-(n-1)qEd （3分）