问题
解答题
已知函数f（x）=x3-ax2-x+a，其中a为实数，
（1）求导数f′（x）；
（2）若f′（-1）=0，求f（x）在[-2，3]上的最大值和最小值；
（3）若f（x）在（-∞，-2]和[3，+∞）上都是递增的，求a的取值范围。
答案
解：（1）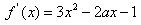
；
（2）
，
∴a=-1，
∴
，
∴
，
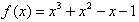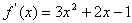由
，
又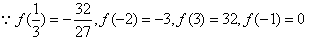
，
∴f（x）在[-2，3]上的最大值是32，最小值是-3。
（3）
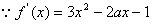图象开口向上，且恒过点（0，-1），
由条件可得：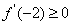
，
，
由
，
∴a的取值范围是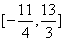
。