问题
解答题
已知函数f（x）=ax3+bx2的图象经过点M（1，4），曲线在点M处的切线恰好与直线x+9y=0垂直．
（1）求实数a，b的值；
（2）若函数f（x）在区间[m，m+1]上单调递增，求m的取值范围．
答案
解：（1）∵f（x）=ax3+bx2的图象经过点M（1，4），
∴a+b ①式
f '（x）=3ax2+2bx，则f '（1）=3a+2b
由条件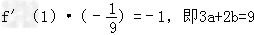
②式
由①②式解得a=1，b=3
（2）f（x）=x3+3x2，f '（x）=3x2+6x，
令f '（x）=3x2+6x≥0 得x≥0或x≤﹣2，
∵函数f（x）在区间[m，m+1]上单调递增
∴[m，m+1]
（﹣∞，﹣2]∪[0，+∞）
∴m≥0或m+1≤﹣2
∴m≥0或m≤﹣3
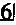时，