问题
选择题
如图所示,匀强电场场强大小为 E ,方向与水平方向夹角为θ(θ≠45°) ,场中有一质量为 m ,电荷量为 q 的带电小球,用长为 L 的细线悬挂于O点,当小球静止时,细线恰好水平.现用一外力将小球沿圆弧缓慢拉到竖直方向最低点,小球电荷量不变,则在此过程中( )

A.外力所做的功为mgLcotθ
B.带电小球的电势能增加 qEL ( sinθ+cosθ)
C.带电小球的电势能增加 2mgLcotθ
D.合外力所做的功为0
答案
AB
分析:对小球进行受力分析可知,小球受重力、电场力及绳子的拉力而处于平衡;由共点力的平衡可求得电场力的大小;
由功的计算公式可求得小球运动中电场力所做的功;则由电场力做功与电势能的关系可求得电势能的变化;再由动能定理可求得外力所做的功.
解答:解:小球在水平位置静止,由共点力的平衡可知,F电sinθ=mg,则F电=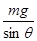 ;
;
小球从最初始位置移到最低点时,电场力所做的功W电=-EqL(cosθ+sinθ),因电场力做负功,故电势能增加,故B正确,C错误;
由动能定理可知,W外+W电+WG=0;
W外=-(W电+W电)=EqL(cosθ+sinθ)-mgL=mgLcotθ;故A正确,D错误;
故选AB.
点评:本题考查了动能定理的应用及电场力做功与电势能的关系,在解题中要注意理解重力做功及电场力做功的特点,正确求得两种功的表达式.
