问题
解答题
设函数f（x）=x3+ax2﹣9x﹣1（a＜0）．若曲线y=f（x）的斜率最小的切线与直线12x+y=6平行，求：
（Ⅰ）a的值；
（Ⅱ）函数f（x）的单调区间．
答案
解：（Ⅰ）因f（x）=x3+ax2﹣9x﹣1
所以f'（x）=3x2+2ax﹣9=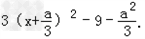
即当x=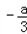
时，f'（x）取得最小值
．
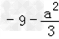因斜率最小的切线与12x+y=6平行，即该切线的斜率为﹣12，
所以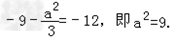
解得a=±3，
由题设a＜0，所以a=﹣3．
（Ⅱ）由（Ⅰ）知a=﹣3，
因此f（x）=x3﹣3x2﹣9x﹣1，f'（x）=3x2﹣6x﹣9=3（x﹣3）（x+1）
令f'（x）=0，解得：x1=﹣1，x2=3．
当x∈（﹣∞，﹣1）时，f'（x）＞0，故f（x）在（﹣∞，﹣1）上为增函数；
当x∈（﹣1，3）时，f'（x）＜0，故f（x）在（﹣1，3）上为减函数；
当x∈（3，+∞）时，f'（x）＞0，故f（x）在（3，+∞）上为增函数．
由此可见，函数f（x）的单调递增区间为（﹣∞，﹣1）和（3，+∞）；
单调递减区间为（﹣1，3）．