问题
证明题
证明：当x＞1时，x＞lnx。
答案
证明：设f（x）=x-lnx，则f′（x）=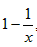
，
∵x＞1，
∴f′（x）＞0，
∴f（x）在（1，+∞）上为增函数，
∴f（x）＞ f（1）=1，
∴x-lnx＞1，
∴x＞lnx+1＞lnx，
即x＞lnx。
搜题请搜索小程序“爱下问搜题”
证明：当x＞1时，x＞lnx。
证明：设f（x）=x-lnx，则f′（x）=，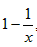
∵x＞1，
∴f′（x）＞0，
∴f（x）在（1，+∞）上为增函数，
∴f（x）＞ f（1）=1，
∴x-lnx＞1，
∴x＞lnx+1＞lnx，
即x＞lnx。