问题
解答题
已知函数f(x)=alnx+x2(a为实常数),
(1)若a=﹣2,求函数f(x)的单调递增区间;
(2)当a<﹣2时,求函数f(x)在[1,e]上的最小值及相应的x值;
(3)若存在x∈[1,e],使得f(x)≤(a+2)x成立,求a的取值范围.
答案
解:(1)a=﹣2,f(x)=﹣2lnx+x2,
∴ ,
,
令f'(x)>0,由x>0得x>1,
∴f(x)的单调递增区间是(1,+∞).
(2) ,
,
令f'(x)=0,由a<﹣2,x>0得
①当 ,即﹣2e2<a<﹣2时,f(x)在
,即﹣2e2<a<﹣2时,f(x)在 递减,在
递减,在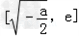 递增,
递增,
∴当 时,
时, .
.
②当 ,即a≤﹣2e2时,f(x)在[1,e]递减,
,即a≤﹣2e2时,f(x)在[1,e]递减,
∴当x=e时,f(x)min=a+e2.
(3)f(x)≤(a+2)x化为:alnx+x2﹣(a+2)x≤0,
设g(x)=alnx+x2﹣(a+2)x,据题意,
当x∈[1,e]时,g(x)min≤0,
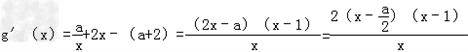 ,
,
(i)当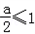 即a≤2时,当x∈[1,e]时,g'(x)≥0,∴g(x)递增,
即a≤2时,当x∈[1,e]时,g'(x)≥0,∴g(x)递增,
∴g(x)min=g(1)=﹣1﹣a≤0,∴a≥﹣1,
∴﹣1≤a≤2;
(ii)当 即2<a<2e时,g(x)在
即2<a<2e时,g(x)在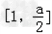 递减,
递减, 递增,
递增,
∴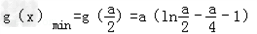 ,
,
∵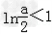 ,∴g(x)min<0,
,∴g(x)min<0,
∴2<a<2e符合题意;
(iii)当 即a≥2e时,g(x)在[1,e]递减,
即a≥2e时,g(x)在[1,e]递减,
∴g(x)min=g(e)=a+e2﹣(a+2)e=(1﹣e)a+e2﹣2e≤2e(1﹣e)+e2﹣2e=﹣e2<0,符合题意,
综上可得,a的取值范围是[﹣1,+∞).
