问题
选择题
某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在三棱柱ABC-A1B1C1的6个点A、B、C、A1、B1、C1上各装一个灯泡,要求同一条线段两端的灯泡不同色,则每种颜色的灯泡都至少用一个的安装方法共有( )
A.215
B.199
C.216
D.305
答案
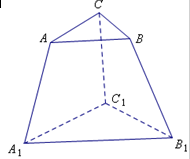
根据题意,每种颜色的灯泡都至少用一个,即用了四种颜色的灯进行安装,分3步进行,
第一步,为A、B、C三点选三种颜色灯泡共有A43种选法;
第二步,在A1、B1、C1中选一个装第4种颜色的灯泡,有3种情况;
第三步,为剩下的两个灯选颜色,假设剩下的为B1、C1,若B1与A同色,则C1只能选B点颜色;若B1与C同色,则C1有A、B处两种颜色可选.故为B1、C1选灯泡共有3种选法,即剩下的两个灯有3种情况,
则共有A43×3×3=216种方法.
故选C.
