问题
解答题
设函数f（x）=（1+x）2-2ln（1+x）．
（1）求f（x）的单调区间；
（2）当0<a<2时，求函数g（x）=f（x）-x2-ax-1在区间[0，3]上的最小值．
答案
（1）定义域为（-1，+∞）．
．
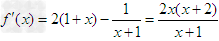令f '（x）>0，则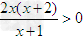
，
所以x<-2或x>0．
因为定义域为（-1，+∞），所以x>0．
令f '（x）<0，则
，所以-2<x<0．
因为定义域为（-1，+∞），所以-1<x<0．
所以函数的单调递增区间为（0，+∞），单调递减区间为（-1，0）．
（2）g（x）=（2-a）x-2ln（1+x），（x>-1）
．
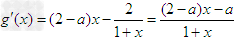因为0<a<2，所以2-a>0，
．
令g’（x）>0， 可得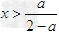
．
所以函数g（x）在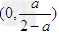
上为减函数，在
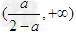上为增函数．
①当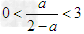
，即
时，
在区间[0，3]上，g（x）在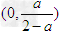
上为减函数，在
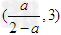上为增函数．
所以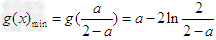
．
②当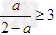
，即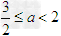
时，g（x）在区间（0，3）上为减函数．
所以g（x）min=g（3）=6-3a-2ln4．
综上所述，当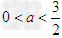
时，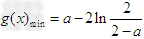
；
当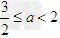
时，g（x）min=g（3）=6-3a-2ln4．