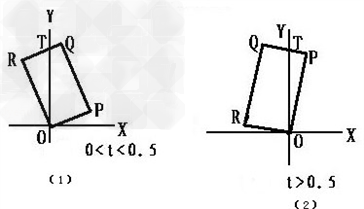问题
解答题
在直角坐标系中，设矩形OPQR的顶点按逆时针顺序依次为O（0，0）、P（1，t）、Q（1﹣2t，2+t）、R（﹣2t，2），其中t∈（0，+∞）．
（1）求矩形OPQR在第一象限部分的面积S（t）；
（2）确定函数S（t）的单调区间，并加以证明．
答案
解：（1）当1﹣2t＞0即0＜t＜
时，0＜t＜
时，点Q在第一象限，如图（1），
直线RQ的方程为y=t（x+2t）+2，它与y轴的交点T（0，2+2t2），
故△ORT的面积S=
×2t×（2+2t2）=2t×（1+t2）
可得矩形在第一象限内的部分面积为S（t）=2+2t2﹣2t×（1+t2）=2[1﹣t×（1+t+t2）]
当﹣2t+1≤0，即t≥
时，如图（2），点Q在y轴上或第二象限，S（t）为△OPT的面积，
直线PQ的方程为y=﹣
+t+
，
令x=0得y=t+
，故点T的坐标为（0，t+
），
故S（t）=S△OPT=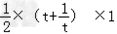
=
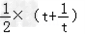
综上知S（t）=
（2）S（t）在区间（0，
）与（
，1）上是减函数，在（1，+∞）是增函数，证明如下
下用导数法证明：由于S'（t）=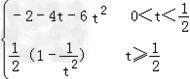
验证知当在区间（0，
）与（
，1）上S'（t）＜0，在（1，+∞）上S'（t）＞0
故得S（t）在区间（0，
）与（
，1）上是减函数，在（1，+∞）是增函数