问题
解答题
定义在R上的函数f（x）=ax3+bx2+cx+3同时满足以下条件：
①f（x）在（0，1）上是减函数，在（1，+∞）上是增函数；
②f′（x）是偶函数；
③f（x）在x=0处的切线与直线y=x+2垂直．
（1）求函数y=f（x）的解析式；
（2）设g（x）=4lnx﹣m，若存在x∈[1，e]，使g（x）＜f′（x），求实数m的取值范围．
答案
解：（1）f'（x）=3ax2+2bx+c
∵f（x）在（0，1）上是减函数，在（1，+∞）上是增函数，
∴f'（1）=3a+2b+c=0…①
由f'（x）是偶函数得：b=0 ②
又f（x）在x=0处的切线与直线y=x+2垂直，f'（0）=c=﹣1③
由①②③得：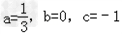
，
即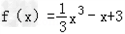
（2）由已知得：若存在x∈[1，e]，使4lnx﹣m＜x2﹣1，
即存在x∈[1，e]，使m＞4lnx﹣x2+1，
设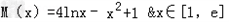
，
则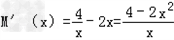
令M'（x）=0，
∵x∈[1，e]，
∴
当
时，M'（x）≤0，
∴M（x）在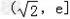
上为减函数
当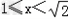
时，M'（x）＞0，
∴M（x）在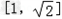
上为增函数
∴M（x）在[1，e]上有最大值．
又M（1）=1﹣1=0，M（e）=2﹣e2＜0，
∴M（x）最小值为2﹣e2
于是有m＞2﹣e2为所求．