问题
解答题
已知函数f（x）=（﹣x2+ax）ex（a∈R）在[﹣1，1]上单调递增，求a的取值范围．
答案
解：∵f（x）=（﹣x2+ax）ex（a∈R），
∴f′（x）=[﹣x2+（a﹣2）x+a]ex，
令g（x）=﹣x2+（a﹣2）x+a，
又f（x）=（﹣x2+ax）ex（a∈R）在[﹣1，1]上单调递增，
∴当x∈[﹣1，1]时，f′（x）≥0，
∴
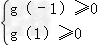，即
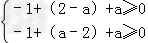，解得a≥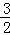 
．
∴a的取值范围为：a≥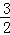
．
