问题
解答题
已知f(x)=x3+bx+cx+d在(﹣∞,0)上是增函数,在[0,2]上是减函数,且方程f(x)=0有三个根,它们分别为α,2,β.
(1)求c的值;
(2)求证f(1)≥2;
(3)求|α﹣β|的取值范围.
答案
解:(1)∵f(x)在(﹣∞,0]上是增函数,在(0,2]上是减函数;
∴x=0是f'(x)=0的根,
又∵f'(x)=3x2+2bx+c,
∴f'(0)=0,∴c=0.
(2)∵f(x)=0的根为α,2,β,
∴f(2)=0,∴8+4b+d=0,
又∵f'(2)≤0,
∴12+4b≤0,∴b≤﹣3,
又d=﹣8﹣4b ∴d≥4 f(1)=1+b+d,f(2)=0
∴d=﹣8﹣4b且b≤﹣3,
∴f(1)=1+b﹣8﹣4b=﹣7﹣3b≥2
(3)∵f(x)=0有三根α,2,β;
∴f(x)=(x﹣α)(x﹣2)(x﹣β) =x3﹣(α+β+2)·x2﹣2αβ
∴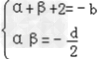 ;
;
∴|β﹣α|2=(α+β)2﹣4αβ =(b+2)2+2d =b2+4b+4﹣16﹣8b
=b2﹣4b﹣12 =(b﹣2)2﹣16
又∵b≤﹣3,∴|β﹣α|≥3
