问题
解答题
设函数f(x)=a2lnx﹣x2+ax,a≠0;
(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)若f(1)≥e﹣1,求使f(x)≤e2对x∈[1,e]恒成立的实数a的值.(注:e为自然对数的底数)
答案
解:(Ⅰ)因为f(x)=a2lnx﹣x2+ax,其中x>0,
所以f'(x)= ﹣2x+a=﹣
﹣2x+a=﹣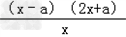 .
.
当a>0时,由f'(x)>0,得0<x<a,
∴f(x)的增区间为(0,a);
当a<0时,由f'(x)>0,得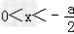 ,
,
∴f(x)的增区间为(0,﹣ );
);
(Ⅱ)由 f(1)=a﹣1≥e﹣1,即a≥e.①
由(Ⅰ)知f(x)在[1,e]内单调递增,要使f(x)≤e2对x∈[1,e]恒成立,
只要f(e)≤e2,
则 a2lne﹣e2+ae≤e2,
∴a2+ae﹣2e2≤0,
∴(a+2e)(a﹣e)≤0,
∴a≤e,②
综①②得a=e
