解：（1）由f'（x）=ln（x+1）+1≥0得 ，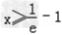

∴f（x）的增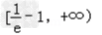区间为 ，减区间为 ．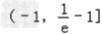

（2）令g（x）=（x+1）ln（x+1）﹣ax．

“不等式f（x）≥ax在x≥0时恒成立”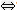“g（x）≥g（0）在x≥0时恒成立．”

g'（x）=ln（x+1）+1﹣a=0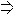x=ea﹣1﹣1．

当x∈（﹣1，e^a﹣1﹣1）时，g'（x）＜0，g（x）为减函数．

当x∈（e^a﹣1﹣1，+∞）时，g'（x）＞0，g（x）为增函数．

“g（x）≥g（0）在x≥0时恒成立”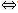“e^a﹣1﹣1≤0”，即e^a﹣1≤e⁰，即a﹣1≤0，即a≤1．

故a的取值范围是（﹣∞，1]．