问题
解答题
已知函数f(x)=x3+2x2﹣ax+1.
(I)若函数f(x)在点(1,f(1))处的切线斜率为4,求实数a的值;
(II)若函数f(x)在区间(﹣1,1)上是单调函数,求实数m的取值范围.
答案
解:(I)f′(x)=3x2+4x﹣a,
k=f′(1)=3+4﹣a=4,故a=3;
(II)f′(x)=3x2+4x﹣a是二次函数,开口向上,对称轴是 x=﹣
要使函数f(x)在区间(﹣1,1)上是单调函数,
只需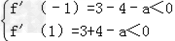
解得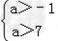 即a>7
即a>7
所以实数a的取值范围是 a>7
