问题
解答题
已知函数f(x)=ax3+bx2+cx在点x0处取得极小值-4,使其导数f'(x)>0的x的取值范围为(1,3),求:
(1)f(x)的解析式;
(2)x∈[2,3],求g(x)=f'(x)+6(m-2)x的最大值.
答案
(1)∵f′(x)=3ax2+2bx+c>0的x的取值范围为(1,3),
∴
,∴b=-6a,c=9a,a<0 -
=1+32b 3a
=1×3c 3a
∴f′(x)=3ax2-12ax+9a=3a(x2-4x+3)=3a(x-1)(x-3),
令f′(x)>0,解得1<x<3;令f′(x)<0,解得x>3,或x<1.
列表如下:
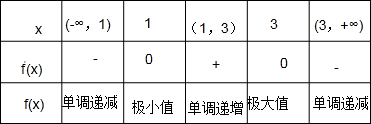
由表格可知:函数f(x)在x=1处取得极小值,∴f(1)=-4,即a-6a+9a=-4,解得a=-1.
∴f(x)=-x3+6x2-9x.
(2)由(1)可得:g(x)=-3x2+12x-9+6(m-2)x
=-3x2+6mx-9
=-3(x-m)2+3m2-9.
①当2≤m≤3时,函数g(x)在区间[2,3]上有:g(x)max=g(m)=-3(m2-2m2+3)=3m2-9.
②当m<2时,g(x)在[2,3]上单调递减,∴g(x)max=g(2)=12m-21.
③当m>3时,g(x)在[2,3]上单调递增,∴g(x)max=g(3)=18m-36.
