问题
解答题
已知函数f（x）=x﹣ax2﹣lnx（a＞0）．
（1）若曲线y=f（x）在点（1，f（1））处的切线斜率为﹣2，求a的值以及切线方程；
（2）若f（x）是单调函数，求a的取值范围．
答案
解：（1）f′（x）=1﹣2ax﹣ 
．
由题设，f′（1）=﹣2a=﹣2，a=1，
此时f（1）=0，切线方程为y=﹣2（x﹣1），即2x+y﹣2=0．
（2）f′（x）=﹣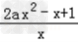
，
令△=1﹣8a．
当a≥ 
时，△≤0，f′（x）≤0，f（x）在（0，+∞）单调递减．
当0＜a＜ 
时，△＞0，方程2ax2﹣x+1=0有两个不相等的正根x1，x2，
不妨设x1＜x2，
则当x∈（0，x1）∪（x2，+∞）时，f′（x）＜0，
当x∈（x1，x2）时，f′（x）＞0，这时f（x）不是单调函数．
综上，a的取值范围是[
，+∞）．