由f（x）=ax²-blnx+2x，得f′(x)=2ax-

b

x

+2=

2ax2+2x-b

x

．

令g（x）=2ax²+2x-b，

因为f（x）=ax²-blnx+2x（a＞0，b＞0）在区间(

1

2

，1)上不单调，

所以在区间(

1

2

，1)上，存在x使得f^′（x）=0，且x不是方程2ax²+2x-b=0的二重根．

即函数g（x）=2ax²+2x-b在区间(

1

2

，1)上有零点，且零点两侧的函数值异号．

又其对称轴方程为x=-

1

2a

＜0，则

g( 1 2 )= a 2 -b+1＜0 g(1)=2a-b+2＞0

．

其可行域如图，

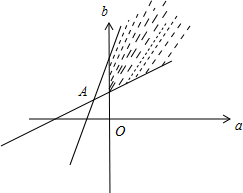
而

3b-2

3a+2

=

b- 2 3

a+ 2 3

，几何意义为可行域内的动点与定点A(-

2

3

，

2

3

)连线的斜率的范围，

由图可知范围为(

1

2

，2)．

故选B．